| Autor: | Fabian Pedregosa |
|---|
Objetivos
Qué es SymPy? SymPy es una biblioteca Python para matemática simbólica. Su propósito es convertirse en un completo sistema de álgebra computacional que pueda competir directamente con alternativas comerciales (Mathematica, Maple) manteniendo, a la vez, el código tan simple como sea posible para hacerlo extensible de manera fácil e integral. SymPy está escrito completamente en Python y no necesita usar otras bibliotecas.
La documentación y los paquetes Sympy para instalarlo pueden encontrarse en: http://sympy.org/
Contenido
SymPy define tres tipos numéricos: Real, Racional y Entero.
La clase Racional representa un número racional como una pareja de números Enteros: el numerador y el denominador, de esta forma Rational(1,2) representa 1/2, Rational(5,2) 5/2, etcétera
>>> from sympy import *
>>> a = Rational(1,2)
>>> a
1/2
>>> a*2
1
SymPy usa mpmath en segundo plano (background), lo que hace posible ejecutar cálculos usando aritmética con precisión arbitraria. De esta forma, algunas constantes especiales como e, pi, oo (Infinito), son tratadas como símbolos y pueden ser evaluadas con precisión arbitraria
>>> pi**2
pi**2
>>> pi.evalf()
3.14159265358979
>>> (pi+exp(1)).evalf()
5.85987448204884
como puedes ver, evalf evalua la expresión como un número decimal.
También existe una clase para representar el infinito (matemático) llamada oo
>>> oo > 99999
True
>>> oo + 1
oo
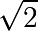con 100 decimales.
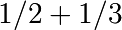en aritmética racional.En contraste a otros sistemas de álgebra computacional, en SymPy hay que declarar las variables simbólicas de forma explícita
>>> from sympy import *
>>> x = Symbol('x')
>>> y = Symbol('y')
Después de declararlas podrán ser usadas
>>> x+y+x-y
2*x
>>> (x+y)**2
(x + y)**2
Los símbolos, ahora, pueden ser manipulados usando algunos de los operadores python: +, -, *, ** (arithmetic), &, |, ~ , >>, << (boolean).
SymPy es capaz de ejecutar potentes manipulaciones algebráicas. Echaremos un vistazo a algunas de las más usadas: expandir y simplificar.
Usa lo siguiente para expandir una expresión algebráica. Tratará de expandir las potencias y multiplicaciones
In [23]: expand((x+y)**3)
Out[23]: 3*x*y**2 + 3*y*x**2 + x**3 + y**3
Se pueden usar diferentes opciones a partir de palabras clave (keywords)
In [28]: expand(x+y, complex=True)
Out[28]: I*im(x) + I*im(y) + re(x) + re(y)
In [30]: expand(cos(x+y), trig=True)
Out[30]: cos(x)*cos(y) - sin(x)*sin(y)
Usa simplify si quieres transformar una expresión en algo más sencillo
In [19]: simplify((x+x*y)/x)
Out[19]: 1 + y
Simplificación es un término vago, es por ello que existen alternativas más precisas que simplify: powsimp (simplificación de exponentes), trigsimp (para expresiones trigonométricas) , logcombine, radsimp, together.
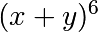.Los límites son fáciles de usar en SymPy, siguen la sintáxis limit(función, variable, punto). Así, para calcular el límite de f(x) como x -> 0, deberías usar la siguiente expresión limit(f, x, 0)
>>> limit(sin(x)/x, x, 0)
1
también puedes calcular el límite en el infinito
>>> limit(x, x, oo)
oo
>>> limit(1/x, x, oo)
0
>>> limit(x**x, x, 0)
1
Puedes derivar cualquier expresión SymPy usando diff(func, var). Ejemplos
>>> diff(sin(x), x)
cos(x)
>>> diff(sin(2*x), x)
2*cos(2*x)
>>> diff(tan(x), x)
1 + tan(x)**2
Puedes comprobar que esto es correcto mediante
>>> limit((tan(x+y)-tan(x))/y, y, 0)
1 + tan(x)**2
Se pueden obtener derivadas de orden superior mediante el método diff(func, var, n)
>>> diff(sin(2*x), x, 1)
2*cos(2*x)
>>> diff(sin(2*x), x, 2)
-4*sin(2*x)
>>> diff(sin(2*x), x, 3)
-8*cos(2*x)
SymPy también permite computar la serie de Taylor de una expresión en un punto. Usa series(expr, var)
>>> series(cos(x), x)
1 - x**2/2 + x**4/24 + O(x**6)
>>> series(1/cos(x), x)
1 + x**2/2 + 5*x**4/24 + O(x**6)
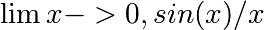
SymPy ofrece soporte para integrales definidas o indefinidas de funciones transcendentes elementales y de funciones especiales via integrate(), que usa una potente extensión del algoritmo Risch-Norman y algo de heurística y de reconocimiento de patrones. Puedes integrar funciones elementales de la siguiente forma
>>> integrate(6*x**5, x)
x**6
>>> integrate(sin(x), x)
-cos(x)
>>> integrate(log(x), x)
-x + x*log(x)
>>> integrate(2*x + sinh(x), x)
cosh(x) + x**2
También se pueden manejar funciones especiales de forma sencilla
>>> integrate(exp(-x**2)*erf(x), x)
pi**(1/2)*erf(x)**2/4
Es posible calcular integrales definidas
>>> integrate(x**3, (x, -1, 1))
0
>>> integrate(sin(x), (x, 0, pi/2))
1
>>> integrate(cos(x), (x, -pi/2, pi/2))
2
También están soportadas las integrales impropias
>>> integrate(exp(-x), (x, 0, oo))
1
>>> integrate(exp(-x**2), (x, -oo, oo))
pi**(1/2)
SymPy es capaz de resolver ecuaciones algebraicas de una o varias variables
In [7]: solve(x**4 - 1, x)
Out[7]: [I, 1, -1, -I]
Como has visto anteriormente, toma una expresión como primer argumento que se supone que es igual a 0. Es capaz de resolver una gran parte de ecuaciones polinómicas. Además, es capar de resolver múltiples ecuaciones respecto a múltiples variables (sistemas de ecuaciones) proporcionando una tupla como segundo argumento
In [8]: solve([x + 5*y - 2, -3*x + 6*y - 15], [x, y])
Out[8]: {y: 1, x: -3}
También tiene capacidad (limitada) de resolver ecuaciones transcendentales
In [9]: solve(exp(x) + 1, x)
Out[9]: [pi*I]
Otra alternativa, en el caso de ecuaciones polinómicas, es factor. factor devuelve el polinomio factorizado en términos irreducibles y es capaz de calcular la factorización sobre varios dominios
In [10]: f = x**4 - 3*x**2 + 1
In [11]: factor(f)
Out[11]: (1 + x - x**2)*(1 - x - x**2)
In [12]: factor(f, modulus=5)
Out[12]: (2 + x)**2*(2 - x)**2
SymPy también resuelve ecuaciones booleanas, esto es, decide si una determinada expresión booleana se cumple o no. Para ello se usa la función satisfiable
In [13]: satisfiable(x & y)
Out[13]: {x: True, y: True}
Lo anterior nos dice que (x & y) es True (verdadero) siempre que ambas variables, x e y, sean True. Si una expresión no puede ser verdadera, i.e. los valores de sus argumentos no pueden hacer que la expresión sea True (verdadera), obtendremos el resultado False (Falso)
In [14]: satisfiable(x & ~x)
Out[14]: False
, 
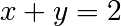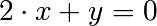
Las Matrices se crean como instancias de la clase Matrix
>>> from sympy import Matrix
>>> Matrix([[1,0], [0,1]])
[1, 0]
[0, 1]
A diferencia de un NumPy array, en una matriz (de Sympy) se pueden incluir también símbolos
>>> x = Symbol('x')
>>> y = Symbol('y')
>>> A = Matrix([[1,x], [y,1]])
>>> A
[1, x]
[y, 1]
>>> A**2
[1 + x*y, 2*x]
[ 2*y, 1 + x*y]
SymPy es capaz de resolver (algunas) ecuaciones diferenciales ordinarias. sympy.ode.dsolve funciona de la siguiente forma
In [4]: f(x).diff(x, x) + f(x)
Out[4]:
2
d
─────(f(x)) + f(x)
dx dx
In [5]: dsolve(f(x).diff(x, x) + f(x), f(x))
Out[5]: C₁*sin(x) + C₂*cos(x)
Se pueden usar argumentos en las keywords para ayudar a encontrar el mejor sistema de resolución posible. Por ejemplo, si a priori conoces que estás tratando con ecuaciones separables, puedes usar la palabra clave (keyword) hint=’separable’ para forzar a dsolve a que lo resuelva como una ecuación separable.
In [6]: dsolve(sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x), f(x), hint='separable')
Out[6]: -log(1 - sin(f(x))**2)/2 == C1 + log(1 - sin(x)**2)/2