Navegación

2.6. Manipulación y procesamiento de imágenes usando Numpy y Scipy

Autores:Emmanuelle Gouillart, Gaël Varoquaux

Imagen = array numérico en 2-D (o 3-D: TC, IRM, 2D + tiempo; 4-D, ...)

Aquí, imagen == array Numpy np.array

Herramientas usadas en este tutorial:

Tareas comunes en procesamiento de imágenes:

  • Entrada, salida y presentación de imágenes
  • Manipulación básica: recortar, girar, rotar, ...
  • Filtrado de imágenes: reducción de ruido, enfoque/refinamiento (sharpening)
  • Segmentación de imágenes: etiquetado de píxeles de acuerdo a los diferentes objetos a que puedan pertenecer
  • Clasificación
  • Extracción/identificación de patrones
  • Registro
  • ...

Existen módulos más potentes y completos:

2.6.1. Abriendo y escribiendo archivos de imágenes

Escribiendo un array a un archivo:

from scipy import misc

l = misc.lena()

misc.imsave('lena.png', l) # uses the Image module (PIL)



import matplotlib.pyplot as plt

plt.imshow(l)

plt.show()
../../_images/lena.png

Creando un array numpy desde un archivo de imagen

>>> lena = misc.imread('lena.png')

>>> type(lena)

<type 'numpy.ndarray'>

>>> lena.shape, lena.dtype

((512, 512), dtype('uint8'))

dtype es uint8 para imágenes de 8-bits (0-255)

Abriendo archivos raw (de cámara, imágenes 3-D)

>>> l.tofile('lena.raw') # Creación de un fichero raw

>>> lena_from_raw = np.fromfile('lena.raw', dtype=np.int64)

>>> lena_from_raw.shape

(262144,)

>>> lena_from_raw.shape = (512, 512)

>>> import os

>>> os.remove('lena.raw')

Necesitas saber la forma y el dtype (tipo de dato) de la imagen (de qué forma separar los bytes de datos).

Para conjuntos de datos de gran tamaño se puede usar np.memmap, que sirve para mapear en memoria estos datos

>>> lena_memmap = np.memmap('lena.raw', dtype=np.int64, shape=(512, 512))

(los datos son leídos desde el archivo, pero no son cargados en la memoria)

Trabajando en una lista de archivos de imágenes

>>> for i in range(10):

...     im = np.random.random_integers(0, 255, 10000).reshape((100, 100))

...     misc.imsave('random_%02d.png' % i, im)

>>> from glob import glob

>>> filelist = glob('random*.png')

>>> filelist.sort()

2.6.2. Mostrando imágenes

Se puede usar matplotlib e imshow para mostrar una imagen dentro de una figura matplotlib

>>> l = scipy.lena()

>>> import matplotlib.pyplot as plt

>>> plt.imshow(l, cmap=plt.cm.gray)

<matplotlib.image.AxesImage object at 0x3c7f710>

Podemos incrementar el contraste ajustando los valores mínimos y máximos

>>> plt.imshow(l, cmap=plt.cm.gray, vmin=30, vmax=200)

<matplotlib.image.AxesImage object at 0x33ef750>

>>> # Remove axes and ticks

>>> plt.axis('off')

(-0.5, 511.5, 511.5, -0.5)

Podemos dibujar las líneas de contorno

>>> plt.contour(l, [60, 211])

<matplotlib.contour.ContourSet instance at 0x33f8c20>
../../_images/plot_display_lena_1.png

[Python source code]

Para hacer una inspección detallada de variaciones de intensidad podemos usar interpolation='nearest'

>>> plt.imshow(l[200:220, 200:220], cmap=plt.cm.gray)

>>> plt.imshow(l[200:220, 200:220], cmap=plt.cm.gray, interpolation='nearest')
../../_images/plot_interpolation_lena_1.png

[Python source code]

A veces, otros paquetes usan paquetes o toolkits para visualización (GTK, Qt)

>>> import scikits.image.io as im_io

>>> im_io.use_plugin('gtk', 'imshow')

>>> im_io.imshow(l)

Visualización en 3-D: Mayavi

Ver Gráficos 3D con Mayavi y Datos volumétricos.

  • Widget para planos de imagen
  • Isosuperficies
  • ...
advanced/image_processing/../3d_plotting/ipw.png

2.6.3. Manipulaciones básicas

Las imágenes las leemos usando arrays numpy: ¡Podemos usar toda la maquinaria numpy!

../../_images/axis_convention.png 
>>> lena = scipy.lena()

>>> lena[0, 40]

166

>>> # Slicing

>>> lena[10:13, 20:23]

array([[158, 156, 157],

[157, 155, 155],

[157, 157, 158]])

>>> lena[100:120] = 255

>>>

>>> lx, ly = lena.shape

>>> X, Y = np.ogrid[0:lx, 0:ly]

>>> mask = (X - lx/2)**2 + (Y - ly/2)**2 > lx*ly/4

>>> # Masks

>>> lena[mask] = 0

>>> # Fancy indexing

>>> lena[range(400), range(400)] = 255
../../_images/plot_numpy_array_1.png

[Python source code]

2.6.3.1. Información estadística

>>> lena = scipy.lena()

>>> lena.mean()

124.04678344726562

>>> lena.max(), lena.min()

(245, 25)

np.histogram

Ejercicio 1

  • Abrimos el logo scikit-image como imagen (http://scikit-image.org/_static/scikits_image_logo.png), o una imagen que tengas en tu computadora.
  • Recortar una parte significativa de la imagen, por ejemplo, el círculo con la python en el logo.
  • Mostrar el array de la imagen usando matlplotlib. Cambia el método de interpolación y haz zoom para ver la diferencia.
  • Transforma tu imagen a escala de grises.
  • Incrementa el contraste de la imagen cambiando sus valores máximo y mínimo. Optional: usa scipy.stats.scoreatpercentile (¡lee el docstring!) para saturar un 5% los píxeles más oscuros y un 5% los píxeles más claros.
  • Guarda el array a los diferentes formatos de imagen (png, jpg, tiff)
advanced/image_processing/scikits_image_logo.png

2.6.3.2. Transformaciones geométricas

>>> lena = scipy.lena()

>>> lx, ly = lena.shape

>>> # Recorte de la imagen

>>> crop_lena = lena[lx/4:-lx/4, ly/4:-ly/4]

>>> # up <-> down flip

>>> flip_ud_lena = np.flipud(lena)

>>> # rotación

>>> rotate_lena = ndimage.rotate(lena, 45)

>>> rotate_lena_noreshape = ndimage.rotate(lena, 45, reshape=False)
../../_images/plot_geom_lena_1.png

[Python source code]

2.6.4. Filtrado de imágenes

Filtros locales: reemplaza el valor de los pixeles por una función de los valores de los pixeles vecinos.

Vecindad: cuadrado (selecciona el tamaño), círculo o elementos estructurados más complejos*.

../../_images/kernels.png

2.6.4.1. Desenfoque/suavizado

Filtro gaussiano de scipy.ndimage

>>> from scipy import misc

>>> lena = misc.lena()

>>> blurred_lena = ndimage.gaussian_filter(lena, sigma=3)

>>> very_blurred = ndimage.gaussian_filter(lena, sigma=5)

Filtro uniforme

>>> local_mean = ndimage.uniform_filter(lena, size=11)
../../_images/plot_blur_1.png

[Python source code]

2.6.4.2. enfoque/refinamiento (sharpening)

Enfocar una imagen borrosa

>>> from scipy import misc

>>> lena = misc.lena()

>>> blurred_l = ndimage.gaussian_filter(lena, 3)

Incrementamos el peso de los bordes agregando una aproximación del laplaciano

>>> filter_blurred_l = ndimage.gaussian_filter(blurred_l, 1)

>>> alpha = 30

>>> sharpened = blurred_l + alpha * (blurred_l - filter_blurred_l)
../../_images/plot_sharpen_1.png

[Python source code]

2.6.4.3. Reduciendo ruido

Imagen de Lena con ruido

>>> from scipy import misc

>>> l = misc.lena()

>>> l = l[230:310, 210:350]

>>> noisy = l + 0.4*l.std()*np.random.random(l.shape)

Un filtro gaussiano suaviza la imagen eliminando el ruido... además de los bordes

>>> gauss_denoised = ndimage.gaussian_filter(noisy, 2)

La mayoría de los filtros lineales isotrópicos locales (ndimage.uniform_filter) desenfocan la imagen.

Un filtro de mediana conserva mejor los bordes

>>> med_denoised = ndimage.median_filter(noisy, 3)
../../_images/plot_lena_denoise_1.png

[Python source code]

Filtro de mediana: mejor resultado para zonas de frontera rectas (baja curvatura)

>>> im = np.zeros((20, 20))

>>> im[5:-5, 5:-5] = 1

>>> im = ndimage.distance_transform_bf(im)

>>> im_noise = im + 0.2*np.random.randn(*im.shape)

>>> im_med = ndimage.median_filter(im_noise, 3)
../../_images/plot_denoising_1.png

[Python source code]

Otros filtros de rango: ndimage.maximum_filter, ndimage.percentile_filter

Otros filtros no lineales locales: Wiener (scipy.signal.wiener), etc.

Filtros no locales

Reducción de ruido de variación total (TV, Total Variation). Encuentra una nueva imagen donde la variación total de la imagen (integral de la norma L1 del gradiente) es minimizada al avez que el resultado se mantiene cercano a la imagen medida

>>> from skimage.filter import tv_denoise

>>> tv_denoised = tv_denoise(noisy, weight=10)

>>> # More denoising (to the expense of fidelity to data)

>>> tv_denoised = tv_denoise(noisy, weight=50)
../../_images/plot_lena_tv_denoise_1.png

[Python source code]

Ejercicio 2: Reducción de ruido

  • Creamos una imagen binaria (de unos y ceros) con varios objetos (círculos, elipses, cuadrados o formas aleatorias).
  • Añadimos algo de ruido (e.g., 20% de ruido)
  • Elige tres métodos para reducir el ruido de la imagen: filtro gaussiano, filtro de la media y el filtro de variación total.
  • Compara los histogramas de las tres imágenes a las que se ha aplicado una reducción de ruido. ¿Qué histograma es el más cercano al de la imagen original (imagen libre de ruido)?

2.6.4.4. Morfología matemática

Ver http://en.wikipedia.org/wiki/Mathematical_morphology

Prueba una imagen con una forma simple (un elemento con estructura) y modifica esta imagen de acuerdo a como se ajuste o no a la imagen.

Elemento con estructura

>>> el = ndimage.generate_binary_structure(2, 1)

>>> el

array([[False,  True, False],

       [ True,  True,  True],

       [False,  True, False]], dtype=bool)

>>> el.astype(np.int)

array([[0, 1, 0],

       [1, 1, 1],

       [0, 1, 0]])
../../_images/diamond_kernel.png

Erosión = filtro mínimo. Reemplaza el valor de un pixel por el valor mínimo del elemento estructurado

>>> a = np.zeros((7,7), dtype=np.int)

>>> a[1:6, 2:5] = 1

>>> a

array([[0, 0, 0, 0, 0, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 0, 0, 0, 0, 0]])

>>> ndimage.binary_erosion(a).astype(a.dtype)

array([[0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 1, 0, 0, 0],

       [0, 0, 0, 1, 0, 0, 0],

       [0, 0, 0, 1, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0]])

>>> #Erosion elimina objectos más pequeños que la estructura

>>> ndimage.binary_erosion(a, structure=np.ones((5,5))).astype(a.dtype)

array([[0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0]])
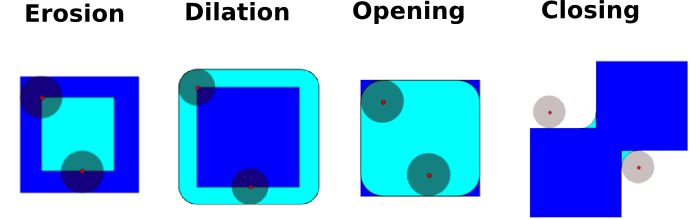
../../_images/morpho_mat.png

Dilatación: filtro máximo

>>> a = np.zeros((5, 5))

>>> a[2, 2] = 1

>>> a

array([[ 0.,  0.,  0.,  0.,  0.],

       [ 0.,  0.,  0.,  0.,  0.],

       [ 0.,  0.,  1.,  0.,  0.],

       [ 0.,  0.,  0.,  0.,  0.],

       [ 0.,  0.,  0.,  0.,  0.]])

>>> ndimage.binary_dilation(a).astype(a.dtype)

array([[ 0.,  0.,  0.,  0.,  0.],

       [ 0.,  0.,  1.,  0.,  0.],

       [ 0.,  1.,  1.,  1.,  0.],

       [ 0.,  0.,  1.,  0.,  0.],

       [ 0.,  0.,  0.,  0.,  0.]])

También funciona para imágenes en escala de grises

>>> np.random.seed(2)

>>> x, y = (63*np.random.random((2, 8))).astype(np.int)

>>> im[x, y] = np.arange(8)



>>> bigger_points = ndimage.grey_dilation(im, size=(5, 5), structure=np.ones((5, 5)))



>>> square = np.zeros((16, 16))

>>> square[4:-4, 4:-4] = 1

>>> dist = ndimage.distance_transform_bf(square)

>>> dilate_dist = ndimage.grey_dilation(dist, size=(3, 3), \

...         structure=np.ones((3, 3)))
../../_images/plot_greyscale_dilation_1.png

[Python source code]

Opening (Apertura): erosión + dilatación

>>> a = np.zeros((5,5), dtype=np.int)

>>> a[1:4, 1:4] = 1; a[4, 4] = 1

>>> a

array([[0, 0, 0, 0, 0],

       [0, 1, 1, 1, 0],

       [0, 1, 1, 1, 0],

       [0, 1, 1, 1, 0],

       [0, 0, 0, 0, 1]])

>>> # Opening removes small objects

>>> ndimage.binary_opening(a, structure=np.ones((3,3))).astype(np.int)

array([[0, 0, 0, 0, 0],

       [0, 1, 1, 1, 0],

       [0, 1, 1, 1, 0],

       [0, 1, 1, 1, 0],

       [0, 0, 0, 0, 0]])

>>> # Opening can also smooth corners

>>> ndimage.binary_opening(a).astype(np.int)

array([[0, 0, 0, 0, 0],

       [0, 0, 1, 0, 0],

       [0, 1, 1, 1, 0],

       [0, 0, 1, 0, 0],

       [0, 0, 0, 0, 0]])

Aplicación (Application): eliminar ruido

>>> square = np.zeros((32, 32))

>>> square[10:-10, 10:-10] = 1

>>> np.random.seed(2)

>>> x, y = (32*np.random.random((2, 20))).astype(np.int)

>>> square[x, y] = 1



>>> open_square = ndimage.binary_opening(square)



>>> eroded_square = ndimage.binary_erosion(square)

>>> reconstruction = ndimage.binary_propagation(eroded_square, mask=square)
../../_images/plot_propagation_1.png

[Python source code]

Cierre (Closing): dilatación + erosión

Esqueletización (Skeletonization): reduce objetos a finas líneas de un píxel de grosor manteniendo la misma topología

Existen muchas otras operaciones matemáticas de morfología: hit and miss transform, tophat, etc.

2.6.5. Extracción de patrones

2.6.5.1. Detección de borde

Datos sintéticos

>>> im = np.zeros((256, 256))

>>> im[64:-64, 64:-64] = 1

>>>

>>> im = ndimage.rotate(im, 15, mode='constant')

>>> im = ndimage.gaussian_filter(im, 8)

Usa un operador gradiente (Sobel) para encontrar altas variaciones de intensidad

>>> sx = ndimage.sobel(im, axis=0, mode='constant')

>>> sy = ndimage.sobel(im, axis=1, mode='constant')

>>> sob = np.hypot(sx, sy)
../../_images/plot_find_edges_1.png

[Python source code]

Filtro de Canny

>>> from skimage.filter import canny

>>> im += 0.1*np.random.random(im.shape)

>>> edges = canny(im, 1, 0.4, 0.2) # not enough smoothing

>>> edges = canny(im, 3, 0.3, 0.2) # better parameters
../../_images/plot_canny_1.png

[Python source code]

Se necesitan ajustar varios parámetros... riesgo de sobreajuste.

2.6.5.2. Segmentación

  • Segmentación basada en histograma (sin información espacial)

    >>> n = 10

    >>> l = 256

    >>> im = np.zeros((l, l))

    >>> np.random.seed(1)

    >>> points = l*np.random.random((2, n**2))

    >>> im[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1

    >>> im = ndimage.gaussian_filter(im, sigma=l/(4.*n))

    

    >>> mask = (im > im.mean()).astype(np.float)

    >>> mask += 0.1 * im

    >>> img = mask + 0.2*np.random.randn(*mask.shape)

    

    >>> hist, bin_edges = np.histogram(img, bins=60)

    >>> bin_centers = 0.5*(bin_edges[:-1] + bin_edges[1:])

    

    >>> binary_img = img > 0.5
../../_images/plot_histo_segmentation_1.png

[Python source code]

Umbral automático: usa el modelo de mezcla gaussiano

>>> mask = (im > im.mean()).astype(np.float)

>>> mask += 0.1 * im

>>> img = mask + 0.3*np.random.randn(*mask.shape)



>>> from sklearn.mixture import GMM

>>> classif = GMM(n_components=2)

>>> classif.fit(img.reshape((img.size, 1))) 

GMM(...)



>>> classif.means

array([[ 0.9353155 ],

       [-0.02966039]])

>>> np.sqrt(classif.covarsi).ravel()

array([ 0.35074631,  0.28225327])

>>> classif.weights

array([ 0.40989799,  0.59010201])

>>> threshold = np.mean(classif.means)

>>> binary_img = img > threshold
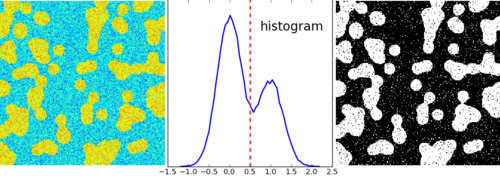
../../_images/image_GMM.png

Usamos morfología matemática para limpiar el resultado

>>> # Elimina pequeñas regiones blancas

>>> open_img = ndimage.binary_opening(binary_img)

>>> # Elimina el pequeño agujero negro

>>> close_img = ndimage.binary_closing(open_img)
../../_images/plot_clean_morpho_1.png

[Python source code]

Ejercicio

Revisa que las operaciones de reconstrucción (erosión + propagación) produzcan un mejor resultado que apertura/cierre (opening/closing)

>>> eroded_img = ndimage.binary_erosion(binary_img)

>>> reconstruct_img = ndimage.binary_propagation(eroded_img, mask=binary_img)

>>> tmp = np.logical_not(reconstruct_img)

>>> eroded_tmp = ndimage.binary_erosion(tmp)

>>> reconstruct_final = np.logical_not(ndimage.binary_propagation(eroded_tmp, mask=tmp))

>>> np.abs(mask - close_img).mean()

0.014678955078125

>>> np.abs(mask - reconstruct_final).mean()

0.0042572021484375

Ejercicio

Revisa cómo un primer paso de reducción de ruido (filtro de mediana, variación total) modifica el histograma y revisa que la segmentación basada en histograma resultante es más exacta.

  • Segmentación basada en gráficos: usa información espacial.
  • Segmentación de línea divisoria (o segmentación watershed)
 >>> from skimage.morphology import watershed, is_local_maximum

 >>>

 >>> # Generate an initial image with two overlapping circles

 >>> x, y = np.indices((80, 80))

 >>> x1, y1, x2, y2 = 28, 28, 44, 52

 >>> r1, r2 = 16, 20

 >>> mask_circle1 = (x - x1)**2 + (y - y1)**2 < r1**2

 >>> mask_circle2 = (x - x2)**2 + (y - y2)**2 < r2**2

 >>> image = np.logical_or(mask_circle1, mask_circle2)

 >>> # Now we want to separate the two objects in image

 >>> # Generate the markers as local maxima of the distance

 >>> # to the background

 >>> from scipy import ndimage

 >>> distance = ndimage.distance_transform_edt(image)

 >>> local_maxi = is_local_maximum(distance, image, np.ones((3, 3)))

 >>> markers = ndimage.label(local_maxi)[0]

>>> labels = watershed(-distance, markers, mask=image)
../../_images/plot_watershed_segmentation_1.png

Segmentation Spectral clustering (cortes normalizados)

>>> from sklearn.feature_extraction import image

>>> from sklearn.cluster import spectral_clustering



>>> l = 100

>>> x, y = np.indices((l, l))



>>> center1 = (28, 24)

>>> center2 = (40, 50)

>>> center3 = (67, 58)

>>> center4 = (24, 70)

>>> radius1, radius2, radius3, radius4 = 16, 14, 15, 14



>>> circle1 = (x - center1[0])**2 + (y - center1[1])**2 < radius1**2

>>> circle2 = (x - center2[0])**2 + (y - center2[1])**2 < radius2**2

>>> circle3 = (x - center3[0])**2 + (y - center3[1])**2 < radius3**2

>>> circle4 = (x - center4[0])**2 + (y - center4[1])**2 < radius4**2



>>> # 4 círculos

>>> img = circle1 + circle2 + circle3 + circle4

>>> mask = img.astype(bool)

>>> img = img.astype(float)



>>> img += 1 + 0.2*np.random.randn(*img.shape)

>>> # Convierte la imagen en un gráfico con el valor del gradiente

>>> # en los bordes.

>>> graph = image.img_to_graph(img, mask=mask)



>>> # Usa una función decreciente del gradiente: we take it weakly

>>> # dependant from the gradient the segmentation is close to a voronoi

>>> graph.data = np.exp(-graph.data/graph.data.std())



>>> labels = spectral_clustering(graph, k=4, mode='arpack')

>>> label_im = -np.ones(mask.shape)

>>> label_im[mask] = labels
../../_images/image_spectral_clustering.png

2.6.6. Midiendo propiedades de objetos: ndimage.measurements

Synthetic data

>>> n = 10

>>> l = 256

>>> im = np.zeros((l, l))

>>> points = l*np.random.random((2, n**2))

>>> im[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1

>>> im = ndimage.gaussian_filter(im, sigma=l/(4.*n))

>>> mask = im > im.mean()

  • Análisis de componentes conectados

    Etiqueta de componentes conectados: ndimage.label

    >>> label_im, nb_labels = ndimage.label(mask)

    >>> nb_labels # how many regions?

    23

    >>> plt.imshow(label_im)        

    <matplotlib.image.AxesImage object at ...>
    ../../_images/plot_synthetic_data_1.png

    [Python source code]

    Calcula tamaño, valor medio, etcétera, de cada región

    >>> sizes = ndimage.sum(mask, label_im, range(nb_labels + 1))

    >>> mean_vals = ndimage.sum(im, label_im, range(1, nb_labels + 1))

    Limpia componentes conectados pequeños

    >>> mask_size = sizes < 1000

    >>> remove_pixel = mask_size[label_im]

    >>> remove_pixel.shape

    (256, 256)

    >>> label_im[remove_pixel] = 0

    >>> plt.imshow(label_im)        

    <matplotlib.image.AxesImage object at ...>

    Ahora reasignamos etiquetas con np.searchsorted

    >>> labels = np.unique(label_im)

    >>> label_im = np.searchsorted(labels, label_im)
    advanced/image_processing/auto_examples/images/plot_measure_data_1.png:scale:90

    [Python source code]

    Encuentra una región de interes del objeto

    >>> slice_x, slice_y = ndimage.find_objects(label_im==4)[0]

    >>> roi = im[slice_x, slice_y]

    >>> plt.imshow(roi)     

    <matplotlib.image.AxesImage object at ...>
    ../../_images/plot_find_object_1.png

    [Python source code]

Otras mediciones espaciales: ndimage.center_of_mass, ndimage.maximum_position, etc.

Pueden ser usadas fuera del limitado campo de acción de las aplicaciones de segmentación.

Ejemplo: bloque promedio

>>> from scipy import misc

>>> l = misc.lena()

>>> sx, sy = l.shape

>>> X, Y = np.ogrid[0:sx, 0:sy]

>>> regions = sy/6 * (X/4) + Y/6  # note that we use broadcasting

>>> block_mean = ndimage.mean(l, labels=regions, index=np.arange(1,

...     regions.max() +1))

>>> block_mean.shape = (sx/4, sy/6)
../../_images/plot_block_mean_1.png

[Python source code]

Cuando las regiones son bloques regulares, es más eficiente usar stride tricks (Example: fake dimensions with strides).

Bloques no espaciados regularmente: promedio radial

>>> sx, sy = l.shape

>>> X, Y = np.ogrid[0:sx, 0:sy]

>>> r = np.hypot(X - sx/2, Y - sy/2)

>>> rbin = (20* r/r.max()).astype(np.int)

>>> radial_mean = ndimage.mean(l, labels=rbin, index=np.arange(1, rbin.max() +1))
../../_images/plot_radial_mean_1.png

[Python source code]

Ejercicio: segmentación

  • Leemos la imagen de las monedas desde skimage (skimage.data.coins) como un array o desde https://github.com/scikits-image/scikits-image/raw/master/skimage/data/coins.png
  • Mostramos el histograma e intentamos hacer una segmentación del histograma.
  • Intenta con dos métodos de segmentación: un método basado en bordes usando skimage.filter.canny y scipy.ndimage.binary_fill_holes y un método basado en regiones skimage.morphology.watershed y skimage.filter.sobel para calcular un mapa de elevaciones.
  • Calcula el tamaño de las monedas.
advanced/image_processing/coins.png

  • Otras mediciones

    Función de correlación, espectro de Fourier/wavelet, etc.

    Un ejemplo con morfología matemática: granulometría (http://en.wikipedia.org/wiki/Granulometry_%28morphology%29)

    >>> def disk_structure(n):

    ...     struct = np.zeros((2 * n + 1, 2 * n + 1))

    ...     x, y = np.indices((2 * n + 1, 2 * n + 1))

    ...     mask = (x - n)**2 + (y - n)**2 <= n**2

    ...     struct[mask] = 1

    ...     return struct.astype(np.bool)

    ...

    >>>

    >>> def granulometry(data, sizes=None):

    ...     s = max(data.shape)

    ...     if sizes == None:

    ...         sizes = range(1, s/2, 2)

    ...     granulo = [ndimage.binary_opening(data, \

    ...         structure=disk_structure(n)).sum() for n in sizes]

    ...     return granulo

    ...

    >>>

    >>> np.random.seed(1)

    >>> n = 10

    >>> l = 256

    >>> im = np.zeros((l, l))

    >>> points = l*np.random.random((2, n**2))

    >>> im[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1

    >>> im = ndimage.gaussian_filter(im, sigma=l/(4.*n))

    >>>

    >>> mask = im > im.mean()

    >>>

    >>> granulo = granulometry(mask, sizes=np.arange(2, 19, 4))
    ../../_images/plot_granulo_1.png

    [Python source code]

Navegación

© Copyright 2012,2013. Creado con Sphinx 1.1.3.